Срочно нужна помощь.... желательно поподробнее расписать. Спасибо)) Окружности радиусов...

Question

Срочно нужна помощь.... желательно поподробнее расписать. Спасибо))
Окружности радиусов 27 и 54 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.

Answer 1

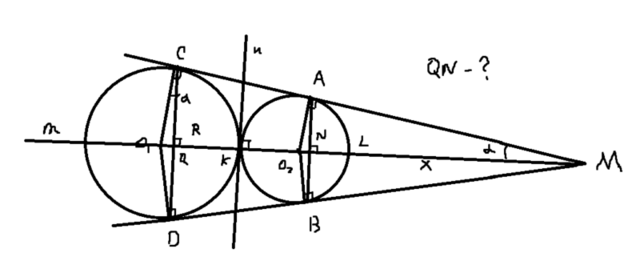
R≡54,r≡27. Пусть # синвол параллельности, ↓ перпендикуляр. R ↓ ac , r ↓ ac ⇒ao2 # co1. (ao2=r , co1=R). o1,o2 ∈ m. Где m=Mo1 и M точка пересечение ac и bd. O1q ↓ cd , O2n ↓ ab. cd # ab. ( cd # n, n↓m ab # n). Значит qn расстояние между ab и cd. Угл cmo2=a ⇒ sin(a)=27/(27+x)=O2n/27 27/(27+x)=54/(108+x). Где x =LM L точка пересечение (o2;r) c m. Sin(a)=O1q/54=O2n/27. Отсюда O2n=9 O1q=18 ⇒ QK=54-18=36. QN= 36+27+9=72. Простите если непонятно писал.

---

Comments

Ответ верный, но немного сложновато решение. Если провести прямую через О2 параллельно касательной АС, то косинус нужного угла α равен отношению разницы радиусов к их сумме, то есть 1/3. Ну и далее через известные величины (радиусы) и этот косинус имеем: QN=O1O2+O2N-O1Q = 81+9-18=72.

---

да ты прав.