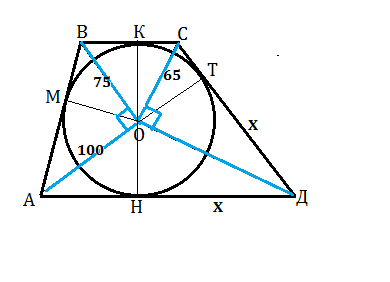
Сделаем и рассмотрим рисунок.
Боковые стороны из центра вписанной в трапецию окружности видны под прямым углом.
Треугольники АОВ и ДОС прямоугольные.
По т.ПифагораАВ= √(ОВ²+ОА²)=125 см
Катет прямоугольного треугольника - среднее пропорциональное между гипотенузой и проекцией на нее этого катета. ВО²=ВМ*АВ
75²=ВМ*125
ВМ=45 ⇒
АМ=125-45=80
Отрезки касательных из одной точки до точек касания равны.⇒
ВК=ВМ=45
АН=АМ=80
По т.Пифагора ОН=60 ( проверьте).
ОК=ОН=60
По т.Пифагора КС=25. ⇒
СТ=25.
Радиус ОТ вписанной окружности - высота прямоугольного треугольника СОД.
Высота прямоугольного треугольника, проведенная из прямого угла - среднее пропорциональное между отрезками, на которые она делит гипотенузу.
ОТ²=СТ*ТД
ТД=ОТ²:СТ=3600:25=144
НД=ТД=144
ВС=ВК+КС=45+25=70
АД=АН+НД=80+144=224
Площадь трапеции равна полусумме оснований, умноженной на высоту.
Высота трапеции равна диаметру вписанной в нее окружности.
S=1/2(BC+АД)*КН= 1/2(70+224)*120=8820