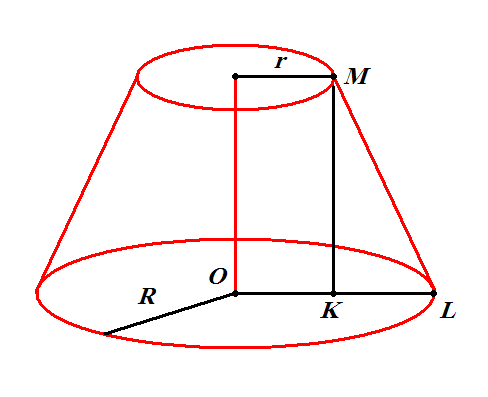
Решение
По формуле длины окружности находим R
C = 2 πR ⇒ R = C/2π ⇒ R = 16π/2π = 8 см.
По теореме Пифагора находим :
(KL) =

(KL) =

см.
(OL) = R = 8 см.
(OK)= R - (KL) = 8 - 6 = 2 см.
⇒ (OK) = r
Осевое сечение есть - трапеция, вычисляем её площадь:

так как a = d = 2r , а b = D = 2R ,то

см²
Ответ: площадь осевого сечения равна 80 см².