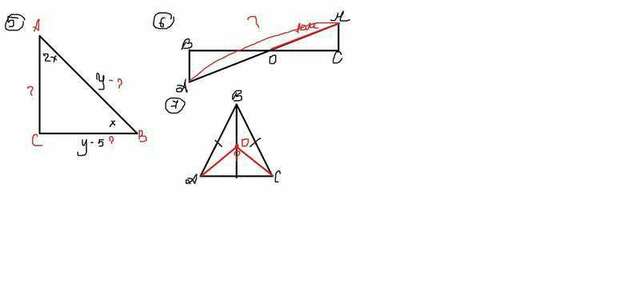
5) Пусть один из острых углов - х, тогда второй - 2х. По свойству острых углов в прямоуг.треугольнике:
х+2х=90
3х=90
х=30 ⇒ Пусть гипотенуза равна у, тогда меньший катет (пусть BC) у-5
Если катет лежит против угла в тридцать градусов, то он равен половине гипотенузы, т.е.:
AC=0.5AB=0.5у
По теореме Пифагора:
АС²+ВС²=АВ²
(0.5у)²+(у-5)²=у²
0.25у²+y²-10y+25=y²
0.25y²-10y+25=0 |×4
y²-40y+100=0
D=1600-400=1200=25×48=5²×4²×3
√D=20√3
y1=(40+20√3)/2=20(2+√3)/2=20+10√3
у2=(40-20√3)/2=20-10√3
Значит, гипотенуза равна или 1)20+10√3 или 2)20-10√3
Найдем меньший катет ВС:
1) ВС=20+10√3 - 5=15+10√3
2) ВС=20-10√3 - 5=15-10√3 (но этот ответ нам не подходит, т.к. √3≈1,73 и тогда ВС=15-10*1.73=15-17.3= - 2.3 < 0 ⇒ АВ≠20-10√3)
Ответ: АВ=20+10√3, ВС=15+10√3
6) Рассмотрим ΔВОА и ΔМОС. Они равны, т.к. у них есть угол по 90* и В равных треугольника соответственные элементы равны, значит, АО=ОМ=1 ⇒ АМ=2ОМ=2
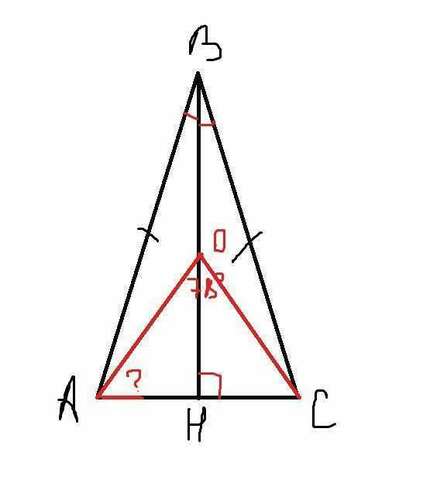
7) [Чертеж на втором рисунке, а то на первом неправильный]
в равнобедренном треугольнике: высота, биссектриса и медиана, исходящие из угла образованного равными сторонами, являются одним и тем же отрезком.
Значит, Δ)