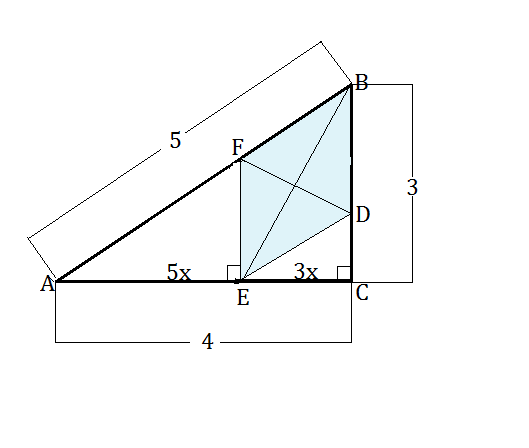
Поскольку вершина треугольника В - вершина ромба, две его стороны - BD и BF лежат на сторонах треугольника ВС и ВА соответственно
ВЕ - диагональ ромба, которая в ромбе является биссектрисой и делит угол АВС пополам.
Биссектриса делит противоположную углу сторону треугольника в отношении прилежащих сторон.
Пусть коэффициент отношения будет х.
Тогда АЕ=5х, ЕС=3х.
АС=4
АЕ+ЕС=8х⇒
х=0,5
АЕ=5*0,5=2,5
Противолежащие стороны ромба параллельны и равны, FЕ || BC ⇒
∠FEА=∠ BCА=90º
EF отсекает от Δ АВС подобный ему треугольник АFE .
Из подобия треугольников
АС:АЕ=ВС:FE
4:2,5=3:FE
4 FE=7,5
FE=1,875 (ед. длины)