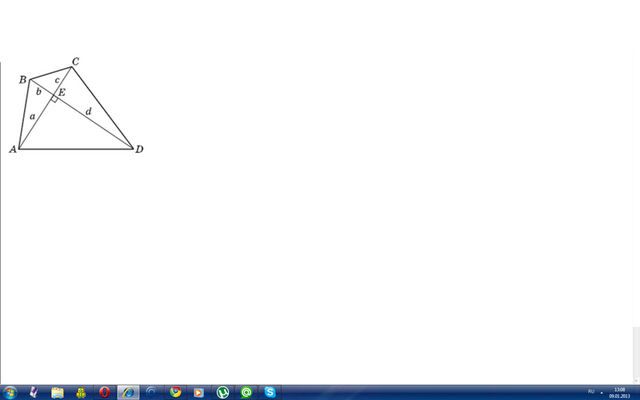
Пусть ABCD — произвольный выпуклый четырехугольник, у которого диагонали взаимно перпендикулярны, пусть E — точка пересечения его диагоналей,
AE = a, BE = b, CE = c, DE = d. Применим к тре угольникам ABE и CDE теорему Пифагора:
AB2 = AE2 + BE2 = a2 + b2,
CD2 = CE2 + DE2 = c2 + d2,
следовательно,
AB2 + CD2 = a2 + b2 + c2 + d2.
Применив теперь теорему Пифагора к треугольникам ADE и BCE, получим:
AD2 = AE2 + DE2 = a2 + d2,
BC2 = BE2 + CE2 = b2 + c2,
откуда вытекает, что
AD2 + BC2 = a2 + b2 + c2 + d2.
Значит, AB2 + CD2 = AD2 + BC2, что и требовалось доказать.