Дано
L₁=20 см =0,2 м длина деревянного цилиндра;
L₂=2,9 см=0,029 см длина выступающей над водой части деревянного цилиндра;
ρ₁=800 кг/м³ плотность дерева
ρ₂=2700 кг/м³ плотность алюминия
ρ=1000 кг/м³ плотность воды
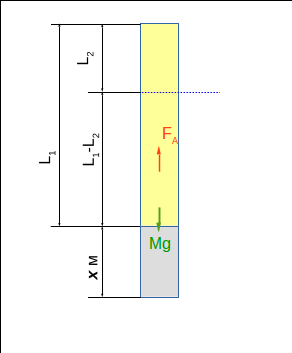
Сообразим рисунок (рисунок 1).
Итак чтобы составной цилиндр при плавал, необходимо, чтобы сила тяжести Mg уравновешивалась силой Архимеда  . Обозначим площадь поперечного сечения S. Тогда в положении требуемого равновесия сила Архимеда.
. Обозначим площадь поперечного сечения S. Тогда в положении требуемого равновесия сила Архимеда.
 (1)
(1)
где V₃ - Объем погруженной части составного цилиндра.
Сила тяжести
 (2)
(2)
Приравниваем правые части (1) и (2) и разрешаем полученное уравнение относительно x.

 (3)
(3)
Подставляем числа в (3)
 м.
м.
Т.е. приблизительно 6,5 мм
P.S.Еще один момент. Для устойчивого вертикального плавания должно выполняться условие: центр плавучести (центр масс вытесненного объема воды должен быть выше, чем центр масс составного цилиндра) .
Проверяем. У нас центр плавучести находится на уровне
(L₁-L₂+x)/2=(0,171+0,0647)/2≈0,0887м от уровня воды. И на таком же расстоянии от нижнего торца
h≈0,0887м=8,87 см.
Положение центра масс составного цилиндра по быстрому определим так:
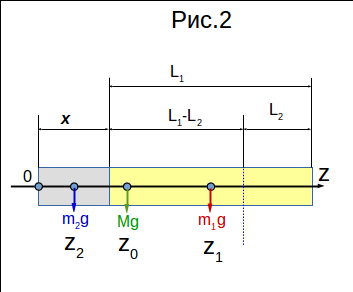
Рассмотрим составной цилиндр в горизонтальном положении (рисунок 2)."Стянем" в точки своих центров масс z₁, z₂ деревянную и алюминиевую части, а затем найдем точку z₀ относительно которой моменты сил F1=m₁g и F2=m₂g , будут равны.
Положение центра масс Z₁=x+L₁/2, соответственно Z₂=x/2
Тогда моменты относительно точки Z₀



z₀≈0,0963м=9,63 см
от нижнего торца. Таким образом центр масс составного цилиндра оказался выше чем центр плавучести (z₀>h), а значит вертикальное положение будет неустойчивым. И, пожалуй, при заданной высоте выступающей части строго вертикального плавания не получится