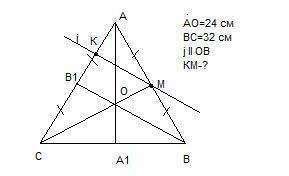
Рассмотрим треугольник АВВ1. Здесь КМ - средняя линия. Мы может это утверждать, если используем теорему Фалеса: если на одной из двух прямых (для нас это АВ) отложить последовательно несколько равных отрезков (это АМ и ВМ, равные по условию) и через их концы провести параллельные прямые, пересекающие вторую прямую (это j и ОВ, пересекающие АС), то они отсекут на второй прямой равные между собой отрезки (т.е. АК=В1К). Если КМ - средняя линия, то
КМ= 1/2ВВ1.
Найдем ВВ1. Рассмотрим треугольник ВА1О. Он прямоугольный, т.к. в равнобедренном треугольнике АВС медиана АА1, проведенная к основанию ВС, является также и высотой.
ВА1=32:2=16 см.
ОА1 можно найти, пользуясь свойством медиан: медианы треугольника пересекаются в одной точке, которая делит кажду медиану в отношении 2 : 1, считая от вершины, т.е.
АО : ОА1 = 2 : 1, отсюда ОА1 = АО : 2 = 24 : 2 = 12 см.
Используя теорему Пифагора, находим ВО в треугольнике ВА1О:
ВО = √BA1²+OA1²=√256+144=√400=20 см.
Снова используем свойство пересекающихся медиан:
ВО : ОВ1 = 2 : 1, отсюда ОВ1 = ВО : 2 = 20 : 2 = 10 см.
ВВ1=ВО+ОВ1=20+10=30 см. Значит
КМ=1/2ВВ1=1/2*30=15 см