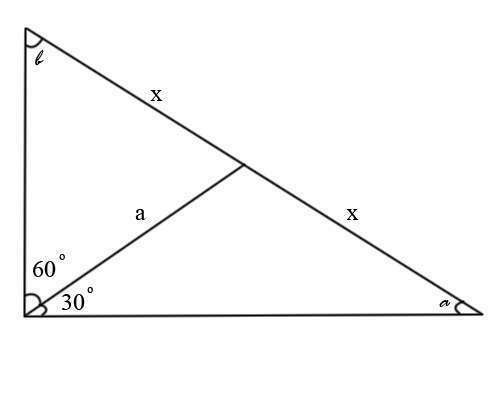
Пусть гипотенуза - 2х, медиана - а. Тогда получается (по свойствам синусов и сторон):
 =
= 
 =
= 
sin 30 = 1/2 sin 60 =  /2
/2
Выразив а из этих уравнений, можно их приравнять. Получаем:
2x*sin a = 
Сократив 2х, выражаем синус одного угла через другой, т. е.
sin b =  *sin a
*sin a
Подбирая значения, получаем угол a = 30 градусам, b = 60
Ответ: наименьший угол равен 30 градусам. Смотри во вложении