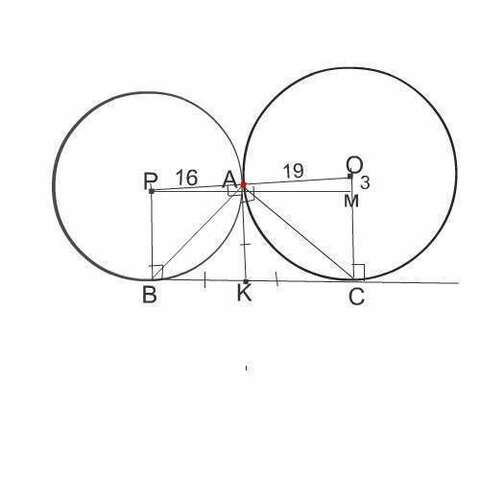
Рассмотрим рисунок.
Точка К - точка вне окружностей, из которой к каждой из них до точек касания В и А к меньшей и до точек С и А к большей идут одинаковой длины отрезки.(по свойству равенства отрезков касательных из одной точки)
КВ=КА.
КА=КС.
ВК=КС
Проведем из центра Р меньшей окружности к радиусу ОС большей окружности перпендикуляр РМ.
Отрезок ОМ равен разности между радиусами окружностей и равен 19-16=3 см
РМ=ВС
РМ по теореме Пифагора из треугольника РОМ равно 8√19
ВК=КС=8√19:2=4√19
АК=ВК=4√19