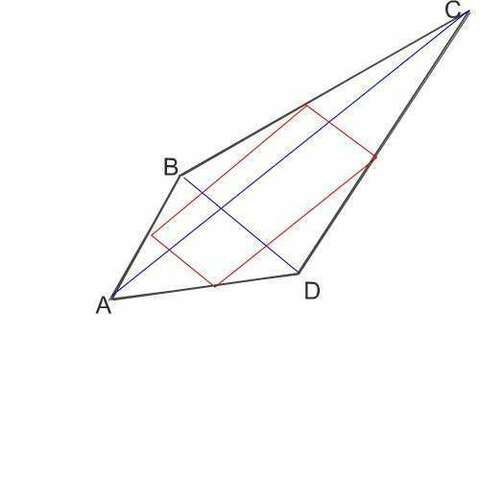
Рассмотрим рисунок.
Красным обозначены отрезки, соединяющие середины сторон четырехугольника АВСD.
Нетрудно заметить, что эти отрезки - средние линии треугольников АВС, АDC, ABD, BCD.
Получившийся четырехугольник имеет две стороны, равные каждая половине BD , и две - равные каждая половине АС.
Следовательно, периметр этого четырехугольника равен сумме диагоналей четырехугольника АВСD и равен 31+9=40.
Кроме того, этот четырехугольник - параллелограмм, т.к. каждая пара противоположных сторон параллельна одной из диагоналей исходного четырехугольника и потому параллельна друг другу.