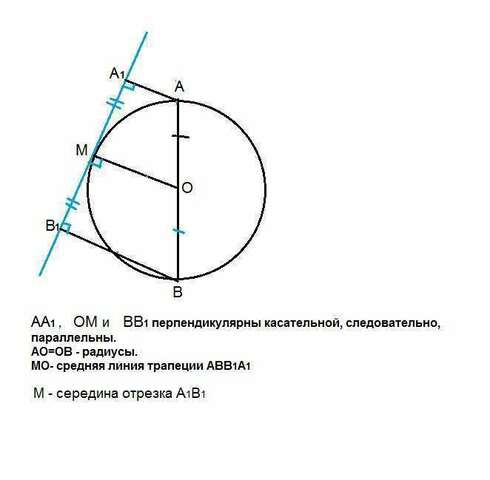
Пусть точка касания отрезка А₁В₁ и окружности будет М.
АА₁ и ВВ₁ перпендикулярны отрезку А₁В₁
ОМ - перпендикулярна А₁В₁ как радиус, проведенный в точку касания.
АА₁, ВВ₁ и ОМ параллельны.
АВВ₁А₁ - прямоугольная трапеция.
Точка О, как центр окружности, делит диаметр АВ пополам.
Т.К ОМ параллельна основаниям, ОМ - средняя линия трапеции. Следовательно, М А₁=МВ₁, что и требовалось доказать.