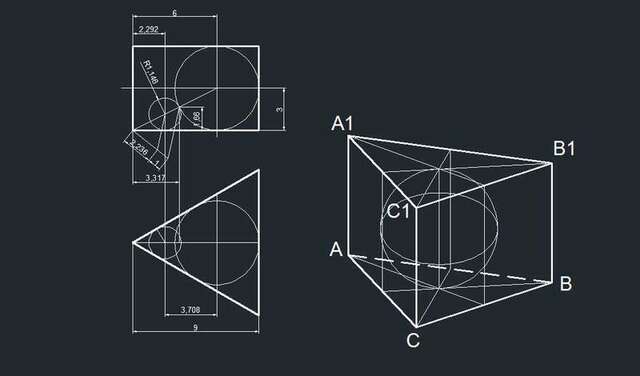
Проведём 2 сечения по призме:
- вертикальное по оси и вершине,
- горизонтальное по оси шара. В сечении равносторонний треугольник с вписанным кругом. Высота в нём равна h = 3R = 9, а расстояние от центра круга до вершины равно (2/3)h = 6.
Примем прямоугольную систему координат с началом в центре шара.
Введём точку М(х;у), в которой меньший шар касается трёх плоскостей призмы и большого шара.
Пусть R - радиус большого шара, r - радиус меньшего шара.
2 шара касаются по линии ОМ = R+r = √(x²+y²) - тут можно на знаки не обращать внимания - квадраты.
Это же расстояние по нормали к плоскости основания можно выразить так:.
√(x²+ y²) = R + (R-y) = 2R - y. Возведём в квадрат обе части:
х² + у² = 4R² -4Ry + y².
После сокращения получаем: 4Ry = 4R² - x².
Отсюда у = (R² - x²) / 4R
Теперь рассмотрим горизонтальное сечение: расстояние от центра меньшего шара до вершины равно 2r как гипотенуза с катетом против угла в 30°. Тогда расстояние 6 = 2r + x, а так как r = 2R - y, то составим систему уравнений:
у = (R² - x²) / 4R
у = (x + 2R -6) / 2. Приравниваем правые части и после приведения к общему знаменателю и сокращения, получаем:
x² + 2Rx - 12R = 0. Так как R =3, то уравнение приобретает вид:
х² + 6х - 36 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=6^2-4*1*(-36)=36-4*(-36)=36-(-4*36)=36-(-144)=36+144=180;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√180-6)/(2*1)=√180/2-6/2=√180/2-3≈3,70820393249935;
x_2=(-√180-6)/(2*1)=-√180/2-6/2=-√180/2-3≈-9,70820393249935.
Отрицательное значение отбрасываем.
Искомый радиус меньшего шара равен r = (6 - x) / 2 =
= (6 - 3,708204) / 2 = 1,145898.