Диагональ правильной четырехугольной призмы равна 18 см, а сторона её основания равна...

$V$ призмы $=S$ осн. $*h$
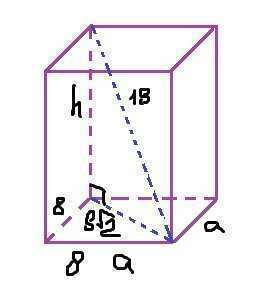
У правильной 4-угольной призмы в основаниях лежат квадраты, а все боковые ребра перпендикулярны основаниям.

(Смотрим рисунок):

Рассмотрим основание: квадрат со стороной $a=8$
Проведём диагональ и найдём её по теореме Пифагора.
$d= \sqrt{8^2+8^2} = \sqrt{8^2*2 } =8 \sqrt{2}$
Площадь квадрата: $S=a^2$
У нас: $S=8^2=64$

Теперь рассмотрим прямоугольный треугольник, который содержит диагональ призмы (равную $18$ по условию), диагональ основания (равную $8 \sqrt{2}$ ) и высоту $h$
Опять же по теореме Пифагора найдем $h$ :
$h= \sqrt{18^2-(8 \sqrt{2})^2 } = \sqrt{324-128} = \sqrt{196} =14$

Теперь вернёмся к нашей формуле объема призмы:

$V=S$ осн. $*h$

Подставим всё:

$V=64*14=896$

Ответ: $896$