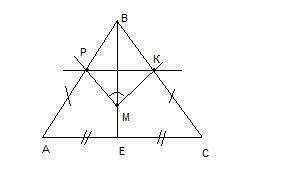
В равнобедренном треугольнике АВС медиана ВЕ, проведенная к основанию АС, является также и биссектрисой, значит
Рассмотрим треугольники МРВ и МКВ. Они равны по стороне и двум прилежащим к ней углам:
- ВМ - общая сторона;
- - У равных треугольников равны соответственные стороны ВР и ВК. Тогда треугольник РВК - равнобедренный, где ВМ - биссектриса, проведенная к его основанию РК (поскольку