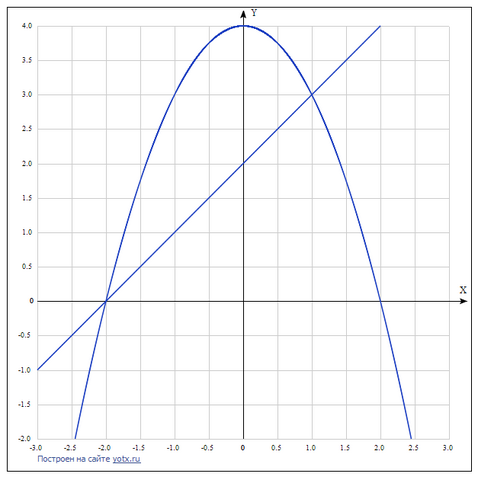
Заданная фигура состоит из двух частей - из треугольника и криволинейной трапеции.
Находим граничные точки.
Крайняя левая точка - пересечение прямой х + 2 с осью ОХ. При этом у = 0, поэтому х + 2 =0 х = -2.
Следующая точка - пресечение прямой х + 2 с параболой 4 - х²:
Приравниваем х + 2 = 4 - х².
х² + х - 2 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=1^2-4*1*(-2)=1-4*(-2)=1-(-4*2)=1-(-8)=1+8=9;
Дискриминант больше 0, уравнение имеет 2 корня:
x₁=(√9-1)/(2*1)=(3-1)/2=2/2=1;
x₂=(-√9-1)/(2*1)=(-3-1)/2=-4/2=-2.
Теперь находим последнюю точку - пересечение параболы с осью ОХ: 4 - х² = 0 х² = 4 х = +-2. Нужна правая точка х = +2,
Площадь левой части (треугольника) S = (1/2)*3*3 = 4.5.
Правая часть: 
4 - 7/3 = 1 2/3 = 1.6667.
Общая площадь равна 4,5 + 1,66667 = 6,1667 кв.ед.