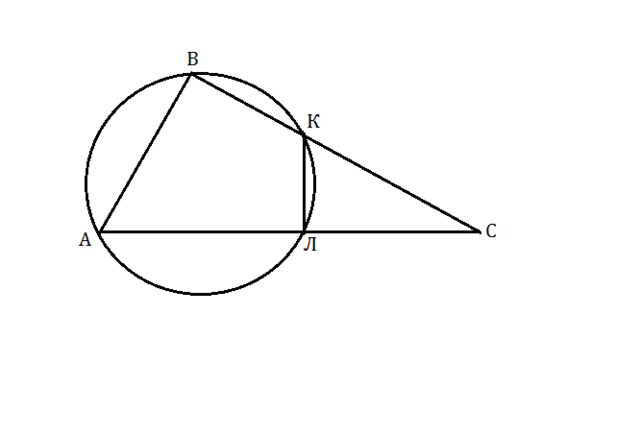
Соединив К и Л, получим вписанный четырехугольник АВКЛ. Четырехугольник может быть вписанным в окружность тогда и только тогда, когда сумма его противоположных углов равна 180º.
Угол ВАЛ+угол ВКЛ=180º
/Угол СКЛ+ угол ВКЛ=180º
Если сумма и одно из слагаемых одного выражения равны сумме и одно из слагаемых второго выражения, то вторые слагаемые тоже равны. ⇒
Угол ВАЛ=углу СКЛ.
В треугольниках АВС и КСЛ угол С - общий, равенство второго угла мы доказали.
Первый признак подобия треугольников:
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны. Ч.т.д.