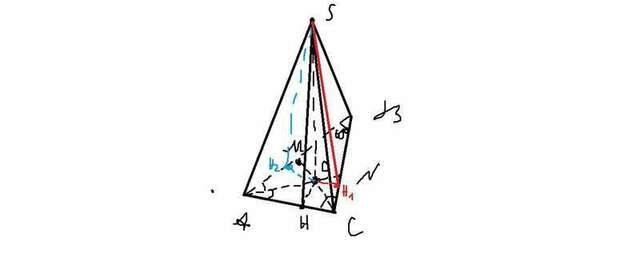
Для начала приложу рисунок к задаче, чтобы лучше понимать суть решения. Задача по сути простая, но объяснений будет много, поскольку упоминается много различных понятий. Посмотрим на примере задачи, как их увязать в одно целое. Итак, рисунок готов.
1)Прежде чем решать задачу, необходимо понять, о чём идёт речь в условии и всё ли мы понимаем. Думаю, насчёт того, что такое пирамида и что такое прямоугольный треугольник, всё ясно. Сделаем рисунок. Прежде всего отмечу, что пирамида не является правильной - это был бы слишком хороший подарок. А вот какая пирамида у нас? Правильно - произвольная. Но вот в этом и есть основная сложность. Ведь если, скажем, у нас дана правильная пирамида, то я знаю о ней довольно много: и что в основании лежит правильный многоугольник, и что вершина пирамиды проецируется в центр основания. Это всё позволяет без труда решать задачи. А вот что здесь? Наверное, первый вопрос, который я хочу прояснить - куда попадёт высота пирамиды? На какую-то точку основания или же промахнётся мимо основания? Это хороший вопрос, потому что существует одна очень важная теорема: если все двугранные углы пирамиды при основании равны, то её вершина проецируется в центр ВПИСАННОЙ окружности основания(на самом деле, это совсем неочевидно, и это надо доказывать. Если появится интерес, обратись ко мне, я покажу, как это сделать) Смотрим в условие - у нас тот самый случай. Значит, говорим мы, вершина пирамиды спроецируется в центр вписанной в треугольник окружности. А вот ещё один вопрос по планиметрии: а где находится эта самая точка? Мы помним, что центром вписанной в треугольник окружности является точка пересечения биссектрис углов треугольника. Значит, проводим в треугольнике ABC биссектрисы CM и AN, они пересекаются в некоторой точке O(двух биссектрис достаточно, так как третья просто пройдёт через точку O). Точка O - центр вписанной в треугольник окружности. Тогда SO - высота пирамиды.
2)Когда мы более менее изобразили на чертеже базовые вещи, пора перейти к тому, что нам требуется найти. Нужно найти площадь боковой поверхности пирамиды. А это что такое? А всё просто - это просто сумма площадей всех боковых граней пирамиды(у нас это три треугольника). Значит, нам надо найти площади трёх боковых треугольников, и сложить их площади. Получим ответ задачи.
3)Приступим. Для начала я хочу построить эти самые углы между плоскостями, о которых идёт речь в задаче. Вспомним определение угла между плоскостями. Это угол между перпендикулярами к линии пересечения плоскостей, проведёнными в этих плоскостях. Иными словами, находим линию пересечения плоскостей, затем берём на ней удобную для нас точку, и в каждой плоскости проводим перпендикуляры к этой линии. Угол между этими перпендикулярами и есть угол между плоскостями. Как применить это определение к нашей задаче?
Построим угол между плоскостями SAC и BAC. Находим их линию пересечения - это AC. Теперь в плоскости ABC проведём к AC перпендикуляр - это OH. Кстати сказать, OH - ещё и радиус вписанной в треугольник окружности. Почему?Потому что окружность касается AC, а радиус окружности, проведённый в точку касания, перпендикулярен касательной. Так что, OH = 3. Теперь в плоскости ASC проведём SH. Докажем, что SH перпендикулярен AC. Замечаем, что AC лежит в плоскости основания, OH - проекция SH на плоскость основания AC перп OH - по построению, значит, в силу теоремы о трёх перпендикулярах SH перп AC. таким образом, мы провели к линии пересечения плоскостей два перпендикуляра, угол между ними и есть угол между плоскостями. То есть, Совершенно аналогично я строю двугранные углы между другими гранями:
4)Теперь найдём все стороны прямоугольного треугольника в основании. AC^2 = 4x^2 - x^2 = 3x^2
AC = xsqrt3
Существует формула, связывающая стороны прямоугольного треугольника с радиусом вписанной в него окружности
r = (a+b-c)/2, где r - радиус вписанной окружности, a,b - катеты, c - гипотенуза. Подставляем, решаем уравнение, находим x:
(x + xsqrt3 - 2x)/2 = 3
(xsqrt3 - x) = 6
x(sqrt3 - 1) = 6
x = 6/(sqrt3 - 1) = BC
Тогда AB = 2x = 12/(sqrt3 - 1), а AC = 6sqrt3/(sqrt3 - 1)
Таким образом, я нашёл все стороны основания, но и ещё основания всех трёх боковых треугольников. Найдём их высоты, тогда можно будет найти их площади.
5)Для этого рассмотрю три прямоугольных треугольника SOH, SOH1 и SOH2. Они, очевидно, равны по двум катетам(катет SO - общий, OH = OH1 = OH2 = 3 - радиусы вписанной окружности). Из равенства этих треугольников вытекает, что высоты всех трёх треугольников равны, то есть SH = SH1 = SH2.