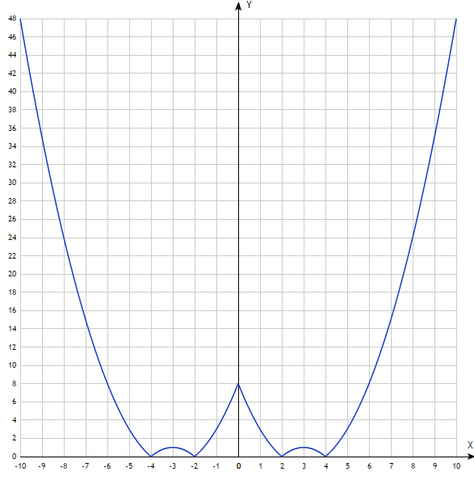
Я бы решал графическим(рисунок во вложении), но представлю другой метод решения.
сделаем замену |x|=t⇒|t²-6t+8|=a
если a<0, уравнение не имеет решения<br>если a=0, то t²-6t+8=0⇒t=4;t=2
x=+-4;x=+-2
таким образом, мы нашли наименьшее значение a, при котором уравнение |x²-6|x|+8|=a будет иметь 4 корня(ибо дальше a>0 нам не имеет смысла рассматривать, раз просят найти наименьшее значение параметра)
насчет графика - его построить относительно просто: строите параболу y=x²-6x+8⇒часть графика при x<0 стираете, а часть при x≥0 отображаете относительно оси Oy⇒часть графика y<0 отображаете вверх относительно оси Ox(часть y≥0 оставить)⇒получили искомый график.<hr>